どさにっきキャッシュレス 〜2019年8月下旬〜

by やまや
<< = >>

2019年8月24日(土)

■ なつやすみのじゆうけんきゅう

_ いや、夏休みどころか完全にカレンダーどおりでお盆もまったく休みなく出社してましたが(仕事したとは言ってない)。

_ それはともかく、自由研究です。お絵かきします。

_ シェルピンスキーのギャスケット。数学的な性質のことは置いておいて、いくつかの方法でこのフラクタル図形を描画するよ。三角形からその中点を結んだ三角形を切り取るという操作を無限に繰り返したもの、というのが定義だけど、この方法はめんどくさいので別の方法で。

■ パスカルの三角形

_ うぃきぺによると パスカルの三角形を作り、奇数を黒、偶数を白で塗りわけるということで可能らしい。まずはこの方法で。

_ まずはパスカルの三角形を作ってみる。8段。 

for i in {0..7};do
  eval echo \$[$p]|xargs -n1|sort|uniq -c|sort -nk2|awk NF--|xargs
  p+="{,+1}"
done
超絶変態的な書き方をしていて bash でしか動かない上、計算量が O(c^n) なのでものすごく遅い。気にしないように。この後もすべてシェルスクリプトだけど、bash の独自拡張を使いまくってるので ash や dash などでは動かない。 
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
偶奇判定させるように書き換えると、シェルピンスキーのギャスケットになる。 
for i in {0..15};do
  eval echo \$[$p]|xargs -n1|sort|uniq -c|sort -nk2|awk '$0=_$1%2'|xargs
  p+="{,+1}"
done|tr 01 \ o
16段に増やすと死ぬほど遅いけどかろうじて動いた。これ以上はやりたくない。最初のパスカルの三角形とは awk の部分が変わっただけ。awk の前が遅いんだからそっちを変えろよ。 
o
o o
o   o
o o o o
o       o
o o     o o
o   o   o   o
o o o o o o o o
o               o
o o             o o
o   o           o   o
o o o o         o o o o
o       o       o       o
o o     o o     o o     o o
o   o   o   o   o   o   o   o
o o o o o o o o o o o o o o o o

■ セルオートマトン

_ 別のアルゴリズムでも描いてみる。うぃきぺの記事には1次元 セルオートマトン(CA)のルール90で描ける、とな。CA は、ある点の現在の周囲の状態により、次の状態が決定されるというモデルで、超有名なものにライフゲームがある。

_ ライフゲームは2次元だけど、今回は1次元 CA。1 が1個だけ、それ以外はぜんぶ 0 という状態から rule 90を適用して、各世代を上から下に順に描画していくと、シェルピンスキーになるそうな。

_ 実際にスクリプトにしてみる前に、ルールを詳しく眺めてみる。 

現在の状態		中央セルの次の状態
111			0
110			1
101			0
100			1
011			1
010			0
001			1
000			0
このルールをよく観察してみると、中央セルの現在の状態が 0、1 どちらかに関係なく、左右のセルの状態にのみ依存して次の状態が決定されることがわかる。ということで、現在の状態から中央セルを削除した表を作ってみる。 
左右セルの現在の状態	中央セルの次の状態
11			0
10			1
01			1
00			0
なんか見覚えがある表が出てきた。これは XOR の真理値表そのものだ。つまり、各セルの状態を c[i] とすると、位置 n の次の世代は c[n-1] ^ c[n+1] で表現されることがわかる(^ は冪乗ではなく xor とする)。

_ ここまでわかったらスクリプトにするのも簡単。 

w=31
c=`printf %0$w\d1%0$w\d`
( echo $c
  for((;j++<w;));do
    c=0$c\0
    t=
    for((i=0;++i<2*w+2;));{
      t+=$[${c:i-1:1}^${c:i+1:1}]	# XOR
    }
    c=$t
    echo $c
  done
)| tr 01 \ o
これを実行するとシェルピンスキーがテキストで出力される。 
                               o
                              o o
                             o   o
                            o o o o
                           o       o
                          o o     o o
                         o   o   o   o
                        o o o o o o o o
                       o               o
                      o o             o o
                     o   o           o   o
                    o o o o         o o o o
                   o       o       o       o
                  o o     o o     o o     o o
                 o   o   o   o   o   o   o   o
                o o o o o o o o o o o o o o o o
               o                               o
              o o                             o o
             o   o                           o   o
            o o o o                         o o o o
           o       o                       o       o
          o o     o o                     o o     o o
         o   o   o   o                   o   o   o   o
        o o o o o o o o                 o o o o o o o o
       o               o               o               o
      o o             o o             o o             o o
     o   o           o   o           o   o           o   o
    o o o o         o o o o         o o o o         o o o o
   o       o       o       o       o       o       o       o
  o o     o o     o o     o o     o o     o o     o o     o o
 o   o   o   o   o   o   o   o   o   o   o   o   o   o   o   o
o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o

_ 視点を変えてみる。

_ 世代が上から下に流れるように表現する場合、あるセルのひとつ前の状態を決定するセルは、そのセルの左上と右上のセルになる。ここで、世代の流れを上から下ではなく、左上から右下に向かうよう変えてみる。すると、あるセルのひとつ前の状態を決定するセルは、そのセルの左と上のセルということになる。つまり、 

c[n] = c[n-1] ^ c[n]
という式であらわせる。これはさらに変形すれば 
c[n] ^= c[n-1]
である。めちゃくちゃ簡単になった。画像の左上のマスに 1 を置き、あとはこの式を繰り返し計算するだけでよい。

_ これをテキストではなく画像ファイルとして出力するシェルスクリプトにしてみたのがこちら。 

! _(){
((____=__,${_______=_____[____]^=_____[____-__],++____<___&&_______}))
$______<<<${_____[@]}
((++________<___))&&_
}
_____=(${__=$?})
___=$[__<<$__$?-__]
: /*/$$;: ${_:__:__}
(${______=/???/???/?$[~__*~__]}<<<${_^}$__\ $___\ $___;_)|convert - sierpinski-ca.png
簡単でしょ？ ちょっと記号が多くて見づらいけど、2行目に xor を計算している ^= という演算子がちゃんと見えるよね。

_ 実行すると以下のような画像が得られる。

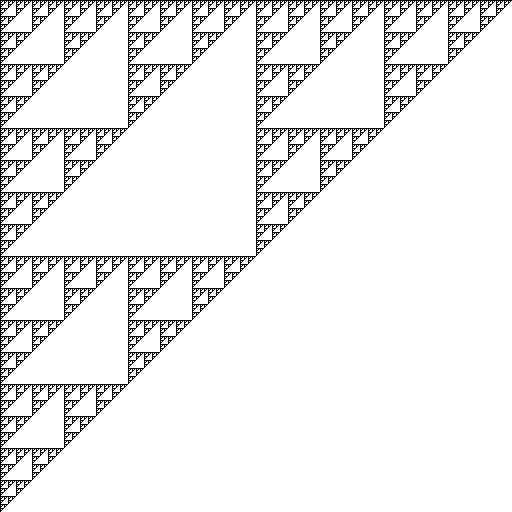
_ なお、このスクリプトを実際に動かすには以下が必要。

■ L-system

_ L-system ってのはさっくり言うと初期状態に一定のルールを繰り返し適用することで複雑な状態を記述するアルゴリズム。厳密な話はよそで調べてくださいませ。今回必要な程度であれば例によって wikipedia の説明で十分。

_ L-system でシェルピンスキーを描画するには、 うぃきぺにもあるとおり、

で描けるそうな。

_ まず置換ルールの部分を書いてみる。m4 で。 

divert(-1)
dnl 置換ルールを指定回数適用させるマクロ
define(`Lsystem', ``$1'
ifelse($2,0,,`Lsystem($1,decr($2))')')
dnl 置換ルール定義
define(`A', ``B - A - B'')
define(`B', ``A + B + A'')
divert(0)dnl
dnl 初期状態 A からルールを3回適用させる
Lsystem(`A', 3)dnl
実行すると以下のようになる。 
A
B - A - B
A + B + A - B - A - B - A + B + A
B - A - B + A + B + A + B - A - B - A + B + A - B - A - B - A + B + A - B - A - B + A + B + A + B - A - B
A -> (B-A-B) -> (A+B+A)-(B-A-B)+(A+B+A) -> ... のように置換がおこなわれていることがわかる。

_ 今度はこれを絵に描く。使うのは ImageMagick の convert コマンド。昔むかし BASIC で LINE 文を連ねて絵を描いていたようなことが、convert でできるのだ。たとえば、 

convert -size 100x100 xc:white -draw "stroke black line 10,10 90,90' line.png
これは 100x100ドットの白い背景の (10,10)-(90,90) に斜めの黒い線をひいて line.png に出力する。詳細は こちら。今回は直進と方向転換のみ、つまり一筆書きでの描画なので、それがやりやすい pathというディレクティブを使う。

_ 完成したスクリプトはこちら。 

# L-system
L=$(m4<<'__END__'|tail -n1
define(`Lsystem', ``$1'
ifelse($2,0,,`Lsystem($1,decr($2))')')
define(`A', ``B - A - B'')
define(`B', ``A + B + A'')
Lsystem(`A', 8)dnl
__END__
)
# 得られた文字列を convert の描画コマンドに
d=(2,0 1,-2 -1,-2 -2,0 -1,2 1,2)
path=$(eval $(echo $L | sed 's/[-+]/((&&i));/g;s/[AB]/echo ${d[i%6]};/g'))
# 描画
convert -size 600x600 xc: -draw "fill none stroke black path 'm50,550 $path'" sierpinski-lsystem.png

_ 実行して得られた画像。左下の頂点から右下の頂点まで、一筆書きで描かれていることがわかるだろうか。三角形から小さな三角形をくりぬくのではなく、このように一筆書きで得られたものを sierpinski arrowhead curveと呼ぶらしい。

_ もうひとつ、同じ L-system で 別のルールでも作れるそうな。

実際に描画するシェルスクリプトと、その結果。上のスクリプトとはパラメータが異なるだけでほとんど同じ中身であることに注目 
L=$(m4<<'__END__'|tail -n1
define(`Lsystem', ``$1'
ifelse($2,0,,`Lsystem($1,decr($2))')')
define(`F', ``F - G + F + G - F'')
define(`G', ``G G'')
Lsystem(`F - G - G', 7)dnl
__END__
)
d=(4,0 -2,4 -2,-4)
path=$(eval $(echo $L | sed 's/[-+]/((&&i));/g;s/[FG]/echo ${d[i%3]};/g'))
convert -size 600x600 xc: -draw "fill none stroke black path 'm50,550 $path'" sierpinski-lsystem2.png

こちらは同じところを複数回通るので数学的な意味では一筆書きではないけど、始点から終点まで筆を離さないということには変わらない。

■ カオスゲームでシェルピンスキーのギャスケット

_ 最後、 カオスゲームという手法。三角形 ABC とその内部の任意の点 P について、

  1. 頂点 ABC のいずれかをランダムで選ぶ
  2. 選んだ頂点と点 P の中点を新たな点 P とする
という手順を何度も繰り返すと、点 P の集合がシェルピンスキーのギャスケットになっちゃうらしい。

_ 3万回繰り返すスクリプトを書いて実行してみる。繰り返し100回ごとに画像を生成し、計300枚の画像を最後に連結して GIF アニメにする。 

x=(250 0 500); y=(33 466 466)			# ABC の X,Y 座標
px=250; py=250					# P の初期座標
for i in {001..300}; do
  for j in {1..100};do
    r=$[RANDOM%3]				# ランダムに頂点を選ぶ
    echo $[px=(px+x[r])/2] $[py=(py+y[r])/2]	# 中点を計算して出力
  done >> tmpfile.$$
  awk '{t[$1+$2*500]=1} END{print "P1",500,500;for(;i++<500^2;)print t[i]?1:0}' < tmpfile.$$ > s$i.pbm
done
convert -delay 3 -layers optimize s???.pbm sierpinski-chaos.gif
rm tmpfile.$$ s???.pbm
実行するとすごーく待たされるけど、生成される GIF アニメの最適化に時間がかかってるだけで、それをやらなければ(-layers optimize を抜けば)そこそこの時間で終わる。ただし、生成される動画サイズが10倍近くになる。

_ 実行結果。

_ 続く。

2019年8月25日(日)

■ マンデルブロ集合

_ ひきつづきシェルスクリプトでお絵かきするよ。今度はシェルピンスキーのギャスケット以外のフラクタル図形を。

_ フラクタルの定番中の定番、マンデルブロ集合でございます。こんな画像。

_ 数学的な性質の詳細はともかく、ただお絵かきするだけなら wikipedia の説明だけで十分。アルゴリズムなんて高尚なものはなく、ひたすら式どおり地道に計算してドットを打つだけ。

_ ということで、上の画像を実際に出力するのに使ったワンライナーがこちら。つーか実質的に dc コマンドを一発叩くだけ(うしろにくっついてる convert は画像フォーマット変換のためのもので、PGM 形式を直接扱える画像ビューワがあるなら不要)。 

dc -e'_2 _1.5 3 512 16 sDsSsWsYsXlD1-lSd[P2]f[lxd*lyd*-la+2lxly**lb+sysxlj1-dsj0!=tlj]sz[lxd*lyd*+4>z]st[0klilS~16klW*lS1-/lX+salW*lS1-/lY+sb0dsxsylDsjlzxpli1+dsilSd*!=m]sm0silmx'|convert - mandelbrot.png
残念ながら一部の Linux distro では dc という超絶ハイパーウルトラ便利なコマンドがデフォでインストールされないという暴挙としか言えない事態になっているので、全人類はいますぐインストールしなさい。

_ 念のため、dc の引数部分を読みやすく整形してコメントを付加したものを載せておく。 

_2 _1.5 3 512 16 sDsSsWsYsX	# X=-2, Y=-1.5, W=3, S=512, D=16
lD1-lSd[P2]f			# PGM ヘッダ
# z: z^2+c
[
  lxd*lyd*-la+			# x=x^2-y^2+a
  2lxly**lb+			# y=2*x*y+b
  sysx
  lj1-dsj 0!=t			# --j != 0 ならマクロ t を実行
  lj				# push j
]sz
[
  lxd*lyd*+4>z			# 発散 (|z|<2) してなければマクロ z を実行
]st
# m: main loop
[
  0klilS~16k                    # i/512, i%512
  lW*lS1-/lX+sa                 # a=(i%512)*3/511-2
  lW*lS1-/lY+sb                 # b=(i/512)*3/511-1.5
  0dsxsylDsj lzx p		# x=y=0, j=16, exec "z", 結果出力
  li1+dsi lSd*!=m		# ++i != 512^2 && exec "m"
]sm
# run
0si lmx				# i=0, exec "m"
先頭の5つのパラメータを変更すると生成される画像が変わる。最初の _2, -1.5 は画像左上の複素座標で、その次の 3 という値を実軸、虚軸に加えたのが画像右下の座標。つまり、(-2-1.5i) - (1+1.5i) の範囲を描画するということ。次の 512 は生成する画像のサイズ、16 は収束したと判断して繰り返しを打ち切る回数で、これは生成されるグレースケール画像の depth としても使われる。

_ もうひとつ別バージョンのマンデルブロ集合描画スクリプト。 

#!/bin/zsh
z='p=x*x-y*y-2+i/66.3,q=2*x*y+1.5-j/66.3,x=p,y=q,--d&&x*x+y*y<4&&z'
f(){ g;((i=0,++j<200))&&f;}
g(){ ((x=0.0,y=0.0,d=16,z));<<<$d;((++i<200))&&g;}
(<<<"P2 200 200 15";f)|convert - mandelbrot-zsh.png
PGM 形式画像の生成を zsh でおこなうシェル(だけ)スクリプト。それを PNG に変換する convert 以外は一切コマンドを呼んでない(zsh のビルトインすら使わない)。整数演算しかできない bash にこんな計算は無理だが、zsh は小数を扱えるのでこんなこともできちゃう。再帰の深さに制限があってデカい画像を作ろうとするとコケるが。

_ 昔書いた awk 版、Lua 版もどうぞ。

■ L-system

_ シェルピンスキーでも使った L-system はもっといろんな画像を作れるのでもうすこしいじってみる。

_ まずは うぃきぺにあるコッホ曲線の例。 

#!/bin/bash
L=$(m4<<'_END_'|tail -n1
define(`Lsystem', ``$1'
ifelse($2,0,,`Lsystem($1,decr($2))')')
define(`F', ``F + F - F - F + F'')
Lsystem(`F', 4)dnl
_END_
)
dir=(10,0 0,-10 -10,0 0,10)
path=$(eval $(echo $L | sed 's/[-+]/((&&i));/g;s/F/echo ${dir[i%4]};/g'))
convert -size 900x500 xc: -draw "fill none stroke black path 'm50,450 $path'"  koch.png
結果。

_ うーん、でも、コッホ曲線って、ふつーは直線を3等分してその真ん中を正三角形の2辺に置き替える、ってものじゃね？ なんか俺が知ってるコッホ曲線と違う。つーことで、見慣れたコッホ曲線を描いてみる。せっかくなので直線ではなく三角形からスタートさせることでコッホ雪片に。

スクリプトのほうは m4 を sed に置き替えてる。やってることは同じ。 
p=F--F--F--
for i in 1 2 3 4 5; do
  p=$(echo $p | sed 's/F/F+F--F+F/g')
done
dir=(2,0 1,-2 -1,-2 -2,0 -1,2 1,2)
path=$(eval $(echo $p | sed 's/[-+]/((&&i));/g;s/F/echo ${dir[i%6]};/g'))
convert -size 600x650 xc:white -draw "fill none stroke black path 'm300,0 $path'" koch-snowflake.png

_ 調子にのってもっとやってみる。

このルールを繰り返し適用すると以下の文字列が得られる。 
A
AB
ABA
ABAAB
ABAABABA
ABAABABAABAAB
ABAABABAABAABABAABABA
ABAABABAABAABABAABABAABAABABAABAAB
前2つの文字列を連結したものが次の文字列になっていて、各文字列の長さは 1, 2, 3, 5, 8, 13, 21, 34, ... すなわちフィボナッチ数列になっている。こういう文字列を Fibonacci word (フィボナッチ列)と呼ぶらしい。

_ このフィボナッチ列を絵にしてみよう。AB はいずれも直進を示すものとする。 ただし、A の方には追加で以下のルールを適用する。

つまり ABAAB なら (直進左折)(直進)(直進左折)(直進右折)(直進) である。

_ スクリプトはこちら。 

p=A
for j in {1..18}; do
  p=$(echo $p | sed 's/A/ab/g;y/B/a/;y/ab/AB/')
done
l=(3,0 0,-3 -3,0 0,3)
A="i+=++n%2?1:-1"	# A なら位置をインクリメントして奇数なら左折、偶数なら右折
B="++n"			# B ならインクリメントだけ
path=$(eval $(echo $p | sed 's/./echo ${l[i%4]};((&));/g'))
convert -size 800x800 xc: -draw "fill none stroke black path 'm50,650 $path'" fibonacci.png
実行すると以下の画像が得られる。fibonacci word fractal と呼ばれ、フィボナッチ数列の特徴が画像中にも見られるらしい。詳細は うぃきぺで。

_ その他 L-system によって生成される画像たち。クリプトは最適化されてだいぶ短かくなってるが、パラメータが異なるだけで、初期状態から置換ルールを数回適用し、得られた文字列を convert の描画コマンドに置き替えるという流れに変わりない。

_ ドラゴン曲線。 

l=(2,2 2,-2 -2,-2 -2,2)
p=FX
eval 'p=$(sed "s/X/x+yF+/g;s/Y/-Fx-y/g;y/xy/XY/"<<<$p);'{,,,,,,,,,,,}
convert -size 550x450 xc: -draw "fill none stroke black path 'm350,350 $(eval $(sed 's/[-+]/((&&i));/g;s/[FXY]/echo ${l[i%4]};/g'<<<$p))'" dragon.png

_ ヒルベルト曲線。 

l=(9,0 0,9 -9,0 0,-9)
p=A
eval 'p=$(sed "s/A/+bF-aFa-Fb+/g;s/B/-aF+bFb+Fa-/g;y/ab/AB/"<<<$p);'{,,,,,}
convert -size 600x600 xc: -draw "fill none stroke black path 'm15,15 $(eval $(sed 's/[-+]/((&&i));/g;s/F/echo ${l[i%4]};/g;s/[AB]//g'<<<$p))'" hilbert.png

_ ゴスペル曲線。 

l=(8,0 4,-7 -4,-7 -8,0 -4,7 4,7)
p=A
eval 'p=`sed "s/A/a-b--b+a++aa+b-/g;s/B/+a-bb--b-a++a+b/g;y/ab/AB/"<<<$p`;'{,,,}
convert -size 500x450 xc: -draw "fill none stroke black path 'm300,10 $(eval `sed 's/[-+]/((&&i));/g;s/[AB]/echo ${l[i%6]};/g'<<<$p`)'" gosper.png

_ ここまでは「直進」と「方向転換」だけで描画したのですべて一筆書き。一筆書き以外の画像を生成するには、「筆を離して別の位置に移動する」という描画ルールが必要になる。

_ ちうことで、以下のルールで絵を描いてみる。 出典はこちら。

[ は現在の位置と方向をスタックに push、] はスタックからの pop をあらわす。通過した場所を覚えておいて(push)、筆を離してその場所に戻ってくる(pop)ってこと。

_ このルールで次数ごとに異なる画像として描画し、さらにそれらを連結して GIF アニメにしてみるスクリプトが以下。実装上の理由により、スクリプト中で push/pop は [] ではなく <> になっている。 

d=(-9 -10 -9 -7 -4 0 4 7 9 10 9 7 4 0 -4 -7)
p=X
for j in {1..5};{
  X=100;Y=750
  p=$(sed "s/F/FF/g;s/X/F+<<X>-X>-F<-FX>+X/g"<<<$p)
  convert -size 800x800 xc: -draw "stroke green $(eval $(sed 's/X//g;s/[-+]/((i&&));/g;s/F/echo line $X,$Y $[X-=d[(i+4)%16]],$[Y+=d[i%16]];/g;s/</S[++s]=\"X=$X;Y=$Y;i=$i\";/g;s/>/eval ${S[s--]};/g'<<<$p))" $j.gif
}
convert -delay 100 ?.gif fractalplant.gif
rm ?.gif

_ 結果。

草生えるwwwwwwwww

_ ペンローズタイルも L-system で記述できる。一連のお絵かきでこれがいちばんスクリプトのサイズがデカいが、それでも550バイトほど。描画する線の色をてきとーに変えてみた。 

x=(21 34 34 21 0 -21 -34 -34 -21 0)
y=(29 11 -11 -29 -36 -29 -11 11 29 36)
M=red;N=blue;O=green;P=purple
X=300;Y=300
p='<N>++<N>++<N>++<N>++<N>'
eval 'p=$(sed "s/M/oA++pA----nA<-oA----mA>++/g;s/N/+oA--pA<---mA--nA>+/g;s/O/-mA++nA<+++oA++pA>-/g;s/P/--oA++++mA<+pA++++nA>--nA/g;s/A//g;y/mnop/MNOP/"<<<$p);'{,,,}
convert -size 600x600 xc: -draw "fill none $(eval $(sed 's/[-+]/((i&&));/g;s/[MNOP]/echo stroke $& line $X,$Y $[X+=x[i%10]],$[Y+=y[i%10]];/g;s/</S[++s]=\"X=$X;Y=$Y;i=$i\";/g;s/>/eval ${S[s--]};/g'<<<$p))" penrosetile.png
結果。

こんな複雑な非周期平面充填図形がたったこれだけのスクリプトで描けるとは。

■ カオスゲーム

_ カオスゲームでシェルピンスキーのギャスケットを描画するには、「点 P とランダムに選んだ三角形の頂点のひとつの中点を新たな P とする」という作業を何度も繰り返すというものだった。

_ これを三角形ではなく正方形にするとどうなるか。こうなる。 

x=100;y=100
for i in {0..9999};do
  echo $[x=(x+RANDOM%2*200)/2] $[y=(y+RANDOM%2*200)/2]
done | awk '{t[$2*200+$1]=1} END{print "P1",200,200;for(;i++<200^2;)print t[i]?1:0}' | convert - chaos-sq.png

むっちゃランダム！

_ が、「同じ頂点を2回続けて選ばない」というルールを追加すると、こうなる。 

x=250;y=250
for i in {0..29999};do
  while :; do t=$[RANDOM%4]; [ "$t" = "$r" ]||break; done; r=$t
  echo $[x=(x+r%2*500)/2] $[y=(y+r/2*500)/2]
done | awk '{t[$1+$2*500]=1} END{print "P1",500,500;for(;i++<500^2;)print t[i]?1:0}' | convert - chaos-sq2.png

むっちゃフラクタル！

_ この手順は 

x(n+1) = a*x(n) + b*y(n) + e
y(n+1) = c*x(n) + d*y(n) + f
という関数を何種類か用意し、その関数のうちひとつをランダムに選択して適用する、と一般化できる。シェルピンスキーのギャスケットを描画するための「ある点と三角形の頂点の中点」なら a=1/2, b=0, c=0, d=1/2 で、e と f が (頂点の座標)/2 という関数を3セット分用意したものに相当する。

_ では、このパラメータを変えるとどうなるか。こうなる。 Bernsley fernと呼ぶらしい。

むっちゃシダ！

_ これを描画するのに使ったワンライナー。 

dc -e'30000[0sa0sb0sc.16sd0sf]s1[.85sa.04sb_.04sc.85sd1.6sf]s2[.02sa_.26sb.23sc.22sd1.6sf]s3[_.15sa.28sb.26sc.24sd.44sf]s4[0k48271lr*2147483647%dsr8/100%9kl1xd1<2d87<394<4lalx*lbly*+dn32Plclx*ldly*lf++psysx1-d0<m]sm0dsxsy12345srlmx'|awk '{p[int($1*50)+int($2*50)*400+3e3]=1}END{print"P1",400,525;for(;i++<21e4;)print p[i]+0}'|convert - +level-colors green,black -flip fern.png
整数しか扱えない bash で小数の計算をさせるのはめんどくさいのでまた dc で。dc 部分をコメントつきで読みやすくしたもの。 
30000				# ループ回数
[ 0sa 0sb 0sc .16sd 0sf ]s1	# 関数 f1-f4 のパラメータ(e は常に 0 なので略)
[ .85sa .04sb _.04sc .85sd 1.6sf ]s2
[ .02sa _.26sb .23sc .22sd 1.6sf ]s3
[ _.15sa .28sb .26sc .24sd .44sf ]s4
# メインループ
[
  0k 48271 lr* 2147483647 %dsr	# 疑似乱数列 (r*48271)%(2^31-1)
  8/ 100% 9k			# 得られた乱数を2桁に
  l1x				# f1
  d1<2				# 乱数が 1 より大きければ f2
  d87<3				# 87 より大きければ f3
  94<4				# 94 よろ大きければ f4
  lalx*lbly*+ dn 32P		# ax+by を計算して出力
  lclx*ldly*lf++ p		# cx+dy+f を計算して出力
  sysx				# 計算結果を新たな x, y に
  1-d0<m			# ループカウンタを減らして0より大きければはじめから
]sm
0dsxsy				# x=0, y=0
12345sr				# 乱数のシード
lmx				# マクロ m を実行

<< = >>
やまや