■ アルゴリズムロールオーバーしてみた。
_ RFC8624 Algorithm Implementation Requirements and Usage Guidance for DNSSEC 曰く、
ということで、推奨されてる ECDSA 鍵が .jp でも 9/19から(やっと)対応したので鍵更新してみた。3.2. DNSKEY Algorithm Recommendation Due to the industry-wide trend towards elliptic curve cryptography, ECDSAP256SHA256 is the RECOMMENDED DNSKEY algorithm for use by new DNSSEC deployments, and users of RSA-based algorithms SHOULD upgrade to ECDSAP256SHA256.
_ 詳しい手順は RFC6781 と RFC7583 を読んでくださいませ。ぶっちゃけロールオーバー作業の細部なんてだいぶ忘れたし、ましてや初めてのアルゴリズムロールオーバーでかなり怪しかったりするけど、Knot DNS に乗り換えて完全にお任せしてるのであまり気にしなくても勝手にやってくれる。
_ まずは knot.conf を修正。
policy:
- id: jp_ecdsa # 新しいポリシー
nsec3: on
ksk-submission: jp
- id: jp_rsasha256 # これまでのポリシー
algorithm: rsasha256
nsec3: on
ksk-lifetime: 365d
ksk-size: 2048
zsk-size: 1024
ksk-submission: jp
cds-cdnskey-publish: none
zone:
- domain: chigumaya.jp
dnssec-signing: on
dnssec-policy: jp_ecdsa # ここを変更
- ksk-lifetime を削除
- もう定期的な KSK ロールオーバーするのはやめる
- その他ロールオーバーまわりのパラメータも削除して knot のデフォルトに合わせる
- cds-cdnskey-publish を削除(デフォルト値に)
- ロールオーバー時だけ CDS、CDNSKEY が見えるように
- レジストリ/レジストラが CDS/CDNSKEY に対応してなければ意味がないのでこれまでは公開しない設定にしていた
- 2.7 までのデフォルトは常時公開だったけど、2.8 のデフォルトはロールオーバー時だけ公開に
- ロールオーバーが終わってしまえば見えなくなるので、デフォでいいや
_ knotc conf-check してエラーがないことを確認したら knotc reload で反映。事前に鍵生成などの作業はしなくてよい。アルゴリズムが変わったことを検知して勝手に鍵を作って勝手にアルゴリズムロールオーバーがはじまる。
鍵ごとに現在のステータスが記録されている。tag 55776 の鍵(KSK)は public とか active とか書いてなくて、ただ作っただけの状態。tag 15948 の鍵(ZSK)は active だから(DNSKEY 以外の)署名には使われるけど鍵自体は publish されておらず外からは見えない、はず。ほんとにそうなってるか dig って確認してみる。Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: control, received command 'reload' Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: reloading configuration file '/usr/local/etc/knot/knot.conf' Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing zone Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, algorithm rollover started Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 55776, algorithm ECDSAP256SHA256, KSK Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 15948, algorithm ECDSAP256SHA256, active+ Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 65044, algorithm RSASHA256, KSK, public, active Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 10774, algorithm RSASHA256, public, active Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing started Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, successfully signed Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, next signing at 2019-09-17T17:55:23 Sep 17 16:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] zone file updated, serial 1568343751 -> 1568706923
ということで、DNSKEY は更新前のアルゴリズム番号 8 の鍵だけ、それ以外のレコードに対する署名は新旧両方の鍵による署名が付与されていてログと一致する。鍵のステータスも同様に。% dig +noall +ans dnskey chigumaya.jp chigumaya.jp. 2242 IN DNSKEY 256 3 8 AwEAAb2dJ2ynrbCCYJkTLsf1CZUtsC72QBH/WZVE7XIrMrIbbe90RcwB AqWfPSBYYbdqJkrbEfikmxWxsQwH4eRio5l0idlhXqo+SeOyXpOdjx8d Z1GyBuwy8hwQsB4xM+5ydvTyB/k950sSzHar2h7VC2+ceRoml/KnjZSK 5SrvqNFV chigumaya.jp. 2242 IN DNSKEY 257 3 8 AwEAAZt3v64lrEhmX572QwKJI2D8TxM4XvJq02CALs7pE0FOyC3/lNb5 lzwg8tAcPQO90c1iSs3O9zm+FOAVP74QLi1tplCDog8+TmEDyfNLvpKq INAk0BDVDRiSlO/r90UafSOk6rQWPYK7DfzBHByoqiWdaIje05WyFtj8 oIZ6pHKiKtZaava471k+szphWi8fq73+aGtI5/ik5SgKI6xWWEwHBf2X bgo10jO/d59Cioxs8/NaUxTY0W9MGxi8q+9y3WBdmF//Z0DG7+ztWpoP GpPY1vdQzO0vjV8YlnEbApy7kN+/1Ujy8TkVI6BfDCf9yypgLPYFqJon kBXhT4BCySc= % dig +noall +ans +dnssec chigumaya.jp chigumaya.jp. 86400 IN A 160.16.73.77 chigumaya.jp. 86400 IN RRSIG A 8 2 86400 20190927020231 20190913003231 10774 chigumaya.jp. A1HQYmpV4uEbgQk7n1czqIRavcaG8EnywwsYt3uHwdqbV7ybaK1hXYjz ZQh08wUXEZX4wq+ks+VfwAnLBU4N9g4RwlnERU3IuH3xnK0bAnveeyc8 bNQsfrZRoTOgGMOYqgeeb7Dg7agEubDhI5OM4LS8z6Rx05Vx+ir3YaCo MfA= chigumaya.jp. 86400 IN RRSIG A 13 2 86400 20191001075523 20190917062523 15948 chigumaya.jp. /CF37jMkanyolNiHRs+zv0VqwqK73t2L+D5+Cv7yNvf+6nvCSgvadQra jH3TBSuU5hh6xFmyfUVHJTztkFgEeQ==
algorithm=13 が新規に作成された ECDSA の鍵で、publish も active も値が入ってない。8 はこれまでの RSA 鍵。# keymgr chigumaya.jp list 6fcf6d0bd8190bae0b6444d00424f287cbebbdac ksk=no zsk=yes tag=15948 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=0 ready=0 active=0 retire-active=0 retire=0 post-active=0 remove=0 a5ae4c186045c36d19014a8e7b2f110fe439b5a3 ksk=yes zsk=no tag=65044 algorithm=8 size=2048 public-only=no pre-active=0 publish=1538445746 ready=1538449346 active=1538485347 retire-active=0 retire=0 post-active=0 remove=0 c0c889cd7b9016269bd31587c611e75108eb1c9d ksk=yes zsk=no tag=55776 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=0 ready=0 active=0 retire-active=0 retire=0 post-active=0 remove=0 cdf6b2aef9df6420dc5bd0cad1e8aee263ee0eb7 ksk=no zsk=yes tag=10774 algorithm=8 size=1024 public-only=no pre-active=0 publish=1567645351 ready=0 active=1567735351 retire-active=0 retire=0 post-active=0 remove=0
_ 1時間後。新旧の鍵が publish され、KSK も active になった。
ちなみに active と active+ の違いはよくわからん(調べろ)。KSK/ZSK ともに active かつ publish されたということは、新鍵が外から見えるようになって、その鍵による RRSIG も付与されてるはず。Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing zone Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 55776, algorithm ECDSAP256SHA256, KSK, public, active+ Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 15948, algorithm ECDSAP256SHA256, public, active+ Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 65044, algorithm RSASHA256, KSK, public, active Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 10774, algorithm RSASHA256, public, active Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing started Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, successfully signed Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, next signing at 2019-09-18T18:55:23 Sep 17 17:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] zone file updated, serial 1568706923 -> 1568710523
はい、そうなってますね。% dig +noall +ans +dnssec chigumaya.jp dnskey chigumaya.jp. 83864 IN DNSKEY 256 3 8 AwEAAb2dJ2ynrbCCYJkTLsf1CZUtsC72QBH/WZVE7XIrMrIbbe90RcwB AqWfPSBYYbdqJkrbEfikmxWxsQwH4eRio5l0idlhXqo+SeOyXpOdjx8d Z1GyBuwy8hwQsB4xM+5ydvTyB/k950sSzHar2h7VC2+ceRoml/KnjZSK 5SrvqNFV chigumaya.jp. 83864 IN DNSKEY 256 3 13 361vuxUWp5cUtlwayVHl7TXqdOWjEM0xBjKmVu3iWhoGDty75cMXckTI gvHsMbx6rbjRagB8fSGEhDvtzM0kGQ== chigumaya.jp. 83864 IN DNSKEY 257 3 8 AwEAAZt3v64lrEhmX572QwKJI2D8TxM4XvJq02CALs7pE0FOyC3/lNb5 lzwg8tAcPQO90c1iSs3O9zm+FOAVP74QLi1tplCDog8+TmEDyfNLvpKq INAk0BDVDRiSlO/r90UafSOk6rQWPYK7DfzBHByoqiWdaIje05WyFtj8 oIZ6pHKiKtZaava471k+szphWi8fq73+aGtI5/ik5SgKI6xWWEwHBf2X bgo10jO/d59Cioxs8/NaUxTY0W9MGxi8q+9y3WBdmF//Z0DG7+ztWpoP GpPY1vdQzO0vjV8YlnEbApy7kN+/1Ujy8TkVI6BfDCf9yypgLPYFqJon kBXhT4BCySc= chigumaya.jp. 83864 IN DNSKEY 257 3 13 RGNT++goDbzeT9tiPTo7cgooSJR5aprAsGHtr6zfPt4zqAT/2iq9bhnN mb59jeTe4K3Zei+myOPADRvvgh0tcw== chigumaya.jp. 83864 IN RRSIG DNSKEY 8 2 86400 20191001085523 20190917072523 65044 chigumaya.jp. GEhis2G6g+OEcJ/2beuBZVlVEi2YwDXE9ELQTM1btQQyrXEU+A44pCRv I2rtDFZ3bH2nQb8KTkXrNr7ZIDlv0XRgRv5KweiGig3GRJOzyxAPBYTs DTRvYBurFAZp7BdLSdS/e+IYHd8fyWs+2fkSvd//zIKFvWe49ZwpobNI 2CQxMdk0+1nXUMS7ow6az5N/JBFLoRKailrSvbGAD2V4/9Nrwx318AAd n2c44tJ3IaFoJHnBWy7MWnrGgQIwIV+2VeBMQnBVngGzQnRvSd5FqBig v6zdinIUgD4YrU10Wu8aJvt+RDOWnWFXKSLE9n5gXdCeDpfsWajOuUCJ ye7rJw== chigumaya.jp. 83864 IN RRSIG DNSKEY 13 2 86400 20191001085523 20190917072523 55776 chigumaya.jp. Wi9hYofK3WcP03nFbJp19bgTxgStdYYFKeTO/+Lyg0cOFCSDzZfTYsE/ M2aU5jzs/dAWVYu3bvn53LH/HD9gFA==
こちらも ECDSA (alg=13) の鍵が publish されました。# keymgr chigumaya.jp list 6fcf6d0bd8190bae0b6444d00424f287cbebbdac ksk=no zsk=yes tag=15948 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=0 active=0 retire-active=0 retire=0 post-active=0 remove=0 a5ae4c186045c36d19014a8e7b2f110fe439b5a3 ksk=yes zsk=no tag=65044 algorithm=8 size=2048 public-only=no pre-active=0 publish=1538445746 ready=1538449346 active=1538485347 retire-active=0 retire=0 post-active=0 remove=0 c0c889cd7b9016269bd31587c611e75108eb1c9d ksk=yes zsk=no tag=55776 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=0 active=0 retire-active=0 retire=0 post-active=0 remove=0 cdf6b2aef9df6420dc5bd0cad1e8aee263ee0eb7 ksk=no zsk=yes tag=10774 algorithm=8 size=1024 public-only=no pre-active=0 publish=1567645351 ready=0 active=1567735351 retire-active=0 retire=0 post-active=0 remove=0
_ 25時間経過。ゾーン内の最大 TTL (24時間) + 余裕をもって1時間、かな? 十分な時間がたって DS レコードを登録する準備ができました。
新 KSK の登録準備が完了(ready)、確認待ち(waiting for confirmation) とログに出てる。Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing zone Sep 18 18:55:23 <daemon.notice> sakura knot[39674]: notice: [chigumaya.jp.] DNSSEC, KSK submission, waiting for confirmation Sep 18 18:55:23 <daemon.notice> sakura knot[39674]: notice: [chigumaya.jp.] DNSSEC, KSK submission, waiting for confirmation Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 55776, algorithm ECDSAP256SHA256, KSK, public, ready, active Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 15948, algorithm ECDSAP256SHA256, public, active Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 65044, algorithm RSASHA256, KSK, public, active Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 10774, algorithm RSASHA256, public, active+ Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing started Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, successfully signed Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, next signing at 2019-09-25T09:56:47 Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] zone file updated, serial 1568768207 -> 1568800523
こっちも KSK が reday に。また、RSA の ZSK がリタイア準備状態に。この後は人間が手作業でレジストラに DS 登録しにいくステップであり、自動化作業はいったん中断されるんだけど、Knot は CDS/CDNSKEY に対応しているので準備できたら自動でゾーンに DS を載せてくれる。ということで CDS を確認してみましょう。# keymgr chigumaya.jp list 6fcf6d0bd8190bae0b6444d00424f287cbebbdac ksk=no zsk=yes tag=15948 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=0 active=1568800523 retire-active=0 retire=0 post-active=0 remove=0 a5ae4c186045c36d19014a8e7b2f110fe439b5a3 ksk=yes zsk=no tag=65044 algorithm=8 size=2048 public-only=no pre-active=0 publish=1538445746 ready=1538449346 active=1538485347 retire-active=0 retire=0 post-active=0 remove=0 c0c889cd7b9016269bd31587c611e75108eb1c9d ksk=yes zsk=no tag=55776 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=1568800523 active=0 retire-active=0 retire=0 post-active=0 remove=0 cdf6b2aef9df6420dc5bd0cad1e8aee263ee0eb7 ksk=no zsk=yes tag=10774 algorithm=8 size=1024 public-only=no pre-active=0 publish=1567645351 ready=0 active=1567735351 retire-active=1568800523 retire=0 post-active=0 remove=0
わーい、載ってる。CDS に対応しているレジストリ/レジストラなら、CDS が存在するかどうか絶えず巡回してくれていて、見つけたら(一定の条件で)自動で登録してくれるはずなんだけど(RFC8078)、実際にそんなことをやってるのは .cz 以外に知らず、少なくとも .jp のレジストリも自分が使ってる指定事業者も対応してないのは確定なので、現実的には CDS に意味はない。ということで、手作業で DS 登録する必要があるのだが、.jp が ECDSA 鍵に対応するのは次の日からなのでそれまでこの状態で放置する。% dig +noall +ans chigumaya.jp cds chigumaya.jp. 0 IN CDS 55776 13 2 71ADAAA442066E05A06BC03EEA348B6873B21FB3AB8D64B6BBAF64C6 39DC9152
_ DS 登録待ちの間、定期的にこういうログが出続けている。
通常なら DS を登録したよ(人間様が作業するフェーズは終わったので自動化作業に戻ってね)、と指示をする必要があるのだが、Knot は賢いので登録が完了して DS がひける状態になってるかどうか自力でチェックして勝手にこちらからボールを奪っていく(ように設定することができる)。で、確認したけどまだ登録されてなかったよと報告するのがこのログ。これは以下のように設定する。Sep 18 18:55:23 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DS check, outgoing, remote 203.119.1.1@53, KSK submission attempt: negative
remote:
- id: a.dns.jp
address: [203.119.1.1, 2001:dc4::1]
submission:
- id: jp
parent: a.dns.jp
policy:
- id: jp_ecdsa
nsec3: on
ksk-submission: jp
_ .jp の ECDSA 対応がはじまる 9/19 になった。新しい DS レコードを登録しにいく。DS 登録はレジストラ経由でおこなうので、レジストリが対応してもレジストラが対応してないと意味ないんだが、JPRS 直営の JPDIRECT はさすがに即日対応してた。無事登録を済ませて(ついでに住所その他が引っ越し前のものだったので変更して)、しばらく待つと新 DS が見えるようになった。
RRSIG の署名アルゴリズムが 13 じゃなくて 8 (RSASHA256) なのはこちらのアルゴリズムロールオーバーとは無関係で、.jp 自体はこれまでどおり RSA 鍵で署名されてるからなので問題ない。% dig +noall +ans chigumaya.jp ds +dnssec @a.dns.jp chigumaya.jp. 7200 IN DS 55776 13 2 71ADAAA442066E05A06BC03EEA348B6873B21FB3AB8D64B6BBAF64C6 39DC9152 chigumaya.jp. 7200 IN RRSIG DS 8 2 7200 20191014174513 20190914174513 42078 jp. eOKVlx6p3OndUpzbZkzLWYRVtt9NmBF460LWY1u64d2REFhOjvUDkXRE JE7C0mnLuHzR4AdslG9vKpuM3V/AoSk8YJl9eVpWA9YVF1ttIPGIQ3Vp NdNrD/SUwgdSkH7Cgc+eLotfkCXehZX6z94n/kjntWRmphOpzz3Mqdz+ dvY=
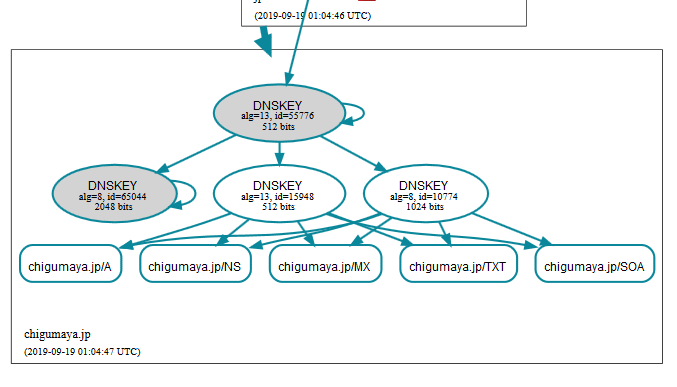
DNSViz で見た直後の鍵の状態。ロールオーバーはじめる前からキャプチャ撮っておけばよかった。
_ ふつーならここで DS 鍵登録終わったよー、自動作業に戻ってねー、と指示するんだけど、前述のようにそれをしなくても勝手に検知する設定を入れてるので待つだけ。
_ ということで待ちました。
外から見える変化はないが、内部的には新しい KSK が上位ゾーン(.jp)に登録されたことを確認したので、旧 KSK をリタイアさせるためのフラグが立った。Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DS check, outgoing, remote 203.119.1.1@53, KSK submission attempt: positive Sep 19 10:55:24 <daemon.notice> sakura knot[39674]: notice: [chigumaya.jp.] DNSSEC, KSK submission, confirmed Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing zone Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 55776, algorithm ECDSAP256SHA256, KSK, public, active Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 15948, algorithm ECDSAP256SHA256, public, active Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 65044, algorithm RSASHA256, KSK, public, active+ Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 10774, algorithm RSASHA256, public, active+ Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing started Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, successfully signed Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, next signing at 2019-09-19T12:55:24 Sep 19 10:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] zone file updated, serial 1568800523 -> 1568858124
外から見える変化はないというのは厳密にはウソで、DS の登録が完了したので不要になった CDS/CDNSKEY がゾーンから取り除かれている(それにともなうゾーン再署名が実行されている)。# keymgr chigumaya.jp list 6fcf6d0bd8190bae0b6444d00424f287cbebbdac ksk=no zsk=yes tag=15948 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=0 active=1568800523 retire-active=0 retire=0 post-active=0 remove=0 a5ae4c186045c36d19014a8e7b2f110fe439b5a3 ksk=yes zsk=no tag=65044 algorithm=8 size=2048 public-only=no pre-active=0 publish=1538445746 ready=1538449346 active=1538485347 retire-active=1568858124 retire=0 post-active=1568865324 remove=0 c0c889cd7b9016269bd31587c611e75108eb1c9d ksk=yes zsk=no tag=55776 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=1568800523 active=1568858124 retire-active=0 retire=0 post-active=0 remove=0 cdf6b2aef9df6420dc5bd0cad1e8aee263ee0eb7 ksk=no zsk=yes tag=10774 algorithm=8 size=1024 public-only=no pre-active=0 publish=1567645351 ready=0 active=1567735351 retire-active=1568800523 retire=0 post-active=1568865324 remove=0
_ 2時間(DS TTL)経過。旧 DS がキャッシュから消えたので、旧 DNSKEY が新たに参照されることはなくなる。よって消す(alg=13 の鍵だけになる)。ただし、キャッシュが残ってる旧 DNSKEY をもとに署名検証される可能性はあるので、旧 DNSKEY による署名は残す。
RSA 鍵のステータスから public が消えている(= 鍵を公開しない)が、ZSK はいまだ active で署名はされる。dig ってみてもたしかにそのとおりになっている。Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing zone Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 55776, algorithm ECDSAP256SHA256, KSK, public, active Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 15948, algorithm ECDSAP256SHA256, public, active Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 65044, algorithm RSASHA256, KSK Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 10774, algorithm RSASHA256, active+ Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing started Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, successfully signed Sep 19 12:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, next signing at 2019-09-20T13:55:24 Sep 19 12:55:25 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] zone file updated, serial 1568858124 -> 1568865324
鍵のステータス。RSA 鍵に post-active のフラグが立った。% dig +noall +ans +dnssec chigumaya.jp dnskey chigumaya.jp. 3260 IN DNSKEY 257 3 13 RGNT++goDbzeT9tiPTo7cgooSJR5aprAsGHtr6zfPt4zqAT/2iq9bhnN mb59jeTe4K3Zei+myOPADRvvgh0tcw== chigumaya.jp. 3260 IN DNSKEY 256 3 13 361vuxUWp5cUtlwayVHl7TXqdOWjEM0xBjKmVu3iWhoGDty75cMXckTI gvHsMbx6rbjRagB8fSGEhDvtzM0kGQ== chigumaya.jp. 3260 IN RRSIG DNSKEY 13 2 86400 20191003035524 20190919022524 55776 chigumaya.jp. /NFpFVc9wegekLxeXeii0SwDd5RIa+uTYKFV2aBllm0GZhyXPrQULyYH ICg9+qjOxMfqpX+OSVANIQDGQj1WlQ== % dig +noall +ans +dnssec chigumaya.jp chigumaya.jp. 3147 IN A 160.16.73.77 chigumaya.jp. 3147 IN RRSIG A 8 2 86400 20191002005647 20190917232647 10774 chigumaya.jp. Q6COWx1FlZKiAHz58n6tmK3BEMIcvVWhvKcJqo3C9i3QZu6XlPXDMPX/ jezc44jBFDwcUb26sEE62vSeuyyZLHF5uUrZ+BKu9FtdqN0aln2bh+T9 ZSlQHcel4V4zi1WhFf0trSMAuWW/wEivxITyWETyOaV9GDBU4Y0ERx0S khk= chigumaya.jp. 3147 IN RRSIG A 13 2 86400 20191002005647 20190917232647 15948 chigumaya.jp. eC3RJcKyAjyGgzBFhxB7wtshDULohi4dLLNtdmzyh/X9zrv1YpHpYbra JbqkToUxzTXcVplhdfUkv8c11VsiBw==
# keymgr chigumaya.jp list 6fcf6d0bd8190bae0b6444d00424f287cbebbdac ksk=no zsk=yes tag=15948 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=0 active=1568800523 retire-active=0 retire=0 post-active=0 remove=0 a5ae4c186045c36d19014a8e7b2f110fe439b5a3 ksk=yes zsk=no tag=65044 algorithm=8 size=2048 public-only=no pre-active=0 publish=1538445746 ready=1538449346 active=1538485347 retire-active=1568858124 retire=0 post-active=1568865324 remove=0 c0c889cd7b9016269bd31587c611e75108eb1c9d ksk=yes zsk=no tag=55776 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=1568800523 active=1568858124 retire-active=0 retire=0 post-active=0 remove=0 cdf6b2aef9df6420dc5bd0cad1e8aee263ee0eb7 ksk=no zsk=yes tag=10774 algorithm=8 size=1024 public-only=no pre-active=0 publish=1567645351 ready=0 active=1567735351 retire-active=1568800523 retire=0 post-active=1568865324 remove=0
_ 25時間後。古い DNSKEY による署名が削除される。ログからついに RSA 鍵の記述が消えた。
keymgr が管理する鍵も ECDSA 鍵だけに。Sep 20 13:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing zone Sep 20 13:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 55776, algorithm ECDSAP256SHA256, KSK, public, active Sep 20 13:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, key, tag 15948, algorithm ECDSAP256SHA256, public, active Sep 20 13:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, signing started Sep 20 13:55:24 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, successfully signed Sep 20 13:55:25 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] DNSSEC, next signing at 2019-09-25T09:56:47 Sep 20 13:55:25 <daemon.info> sakura knot[39674]: info: [chigumaya.jp.] zone file updated, serial 1568865324 -> 1568955324
dig っても ECDSA な RRSIG だけ。# keymgr chigumaya.jp list 6fcf6d0bd8190bae0b6444d00424f287cbebbdac ksk=no zsk=yes tag=15948 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=0 active=1568800523 retire-active=0 retire=0 post-active=0 remove=0 c0c889cd7b9016269bd31587c611e75108eb1c9d ksk=yes zsk=no tag=55776 algorithm=13 size=256 public-only=no pre-active=1568706923 publish=1568710523 ready=1568800523 active=1568858124 retire-active=0 retire=0 post-active=0 remove=0
これにてアルゴリズムロールオーバー終了であります。% dig +noall +ans +dnssec chigumaya.jp chigumaya.jp. 86400 IN A 160.16.73.77 chigumaya.jp. 86400 IN RRSIG A 13 2 86400 20191002005647 20190917232647 15948 chigumaya.jp. eC3RJcKyAjyGgzBFhxB7wtshDULohi4dLLNtdmzyh/X9zrv1YpHpYbra JbqkToUxzTXcVplhdfUkv8c11VsiBw==
_ 長々と過程を記録してきたけど、基本的には変化していく状況を見守ってるだけで、実際に手を動かすのは最初の設定変更と DS 鍵登録の2回だけ。それ以外はすべて Knot が勝手にやってくれる。むちゃくちゃ楽ちん。定期的な KSK ロールオーバーももうやらないことにしたので(ルートゾーンの KSK だって8年使ったんだし、こんな泡沫サイトなんて鍵が漏洩した可能性が高い場合やアルゴリズムが危殆化しないかぎり放置してたって問題にならん)、今後必要な作業は ZSK のロールオーバーと定期的/ゾーン更新時の再署名だけ。これはどちらも完全自動化されてるので、つまり人間はもう何もしなくていいということ。DNSSEC がめんどくさいとかいうのはとっくに過去のものになっており、今は設定を書いたら以後放置プレイでいけるぐらい気楽にできるようになってる。
_ 宗教的な理由で DNSSEC が禁じられてるとか、改竄されても困らないドメインだから必要ないという人にまでやれというつもりはないけど、自動化できる環境がここまで揃ってるのに手間がかかるからとか複雑すぎるからとかいう理由で DNSSEC をやらないのは、もはや時代遅れの言い訳にすぎない。